Contents
Learning Outcomes
-
- To explain the need of a universal system of measurements in science.
- To recall the metric base units and their prefixes.
- To be able to make metric conversions.
- To carry out calculations using numbers in scientific notation.
- To appreciate the difference between Precision and Accuracy
- To be able to record and calculate data with proper significant figures.
- To learn about the key steps in the scientific method
- To identify and list the variables in an experiment
- To identify the parts of graphs and draw graphs based on a given data set.
Prelab
How tall are you? __________
How much do you weight? (we will not double check so feel free to be creative) _________
How much liquid is in a can of soda? ____________
How much rice is in the bag you just got at the store? ___________
What units did you use to answer these questions? ________________
Look at the can of soda or rice bag (or any other item you choose for the exercise).
What units do you find on the container?
What is the difference?
Have you heard of Imperial Units and Metric Units? Which one on the can of soda do you think is an Imperial Unit and which is a Metric Unit?
Imperial: Metric:
Which one do you think is the system that we will be using in our class? __________________
The standard system of measurement in the sciences, including biology, chemistry, and physics is the metric system, which, you may have learned from the prelab exercise, it is not what you use in your everyday life in the USA.
In 1975, the U.S. Metric Conversion Act was signed, declaring a national policy of “encouraging” voluntary use of the metric system. As you may have deduced, the switch from one system to the other did not really work and today, the United States is the only country in the world not committed to adopting the system.
To give you an idea of how the two system differ you can look at Tables 1.1 and 1.2. In Table 1.1 you can see the conversion between Imperial (sometimes you will find it as English system) and Metric system units. In table 1.2 you will find some examples of everyday measurements in the Metric system.
Table 1.1 Conversion between the Imperial and the metric system
| Metric | Imperial |
| 1 cm | 0.4 inch |
| 2.54 cm | 1 inch |
| 1 m | 1.1 yard |
| 1 km | 0.62 mile |
| 1.6 km | 1 mile |
| 1 °C | 9/5 + 32 °F |
| 1 L | 1.06 quart |
| 3.8 L | 1 gallon |
| 28.35 g | 1 oz |
| 453.6 g | 1 lb. |
| 1 kg | 2.2 lb. |
Exercise:
| Temperature |
|
|
|
| Length |
|
|
|
| Mass |
|
|
|
| Volume |
|
Fill in the blanks in the table using the corresponding Imperial or metric system: ex. Water freezes at 32 °F
Looking at Table 1.1 and 1.2 can you list on or two interesting difference between the two systems that you can see?
The metric system is based on decimals or powers of 10.
This 10-based system is similar to our monetary system. Think
How many cents do you have in a dime? ____ cents = 1 dime
How many dimes to you have in a dollar? ____ dimes = 1 dollar.
The great thing about this type of system is that all conversions (going from one unit to the other) are in units of ten.
The refined version of the metric system used in science is called the International System of Units (abbreviated SI).
Metric base units and their prefixes
In biology, often we need to describe measurements of length, volume, mass, time, temperature or amount of substance. In Table 1.3 you can find the whole list of SI Units.
Table 1.3. International System of Units
Metric Units for Biology:
-
- length: meter (m)
-
- Liquid volume: liter (L)
-
- mass: gram (g)
-
- time: second (s)
-
- temperature: Celsius (°C)
- Kelvin (K) is a unit of thermodynamic temperature and is the SI unit. The Kelvin scale is the same as the Celsius or centigrade scale but offset by 273.16, which means that 0 K is – 273.16°C. Biology uses Celsius because of the range of temperatures in which organisms live. Ex. average body temperature is 37°C, Room Temperature is 25°C, water boils at 100°C and freezes at 0°C
- temperature: Celsius (°C)
- amount of substance: mole (mol). A mole is a number representing 6.022×1023 of something. Ex. A pair of shoes equals 2 shoes, a mole of shoes is 6.022×1023 shoes. A dozen eggs equals 12 eggs, a mole of eggs is 6.022×1023 eggs
The metric system is based on the decimal system and follows a consistent name scheme using prefixes that indicates either a multiple of a unit or a fraction of a unit. Multiples and fractions are always expressed as powers of 10. For example, kilogram means a thousand (103) grams, megabyte means a million (106) bytes; centimeter means a hundredth (10-2) of a meter, milliliter means a thousandth (10-3) of a liter. You can find all the prefixes in Table 1.4. The highlighted ones are the most used.
Table 1.4 Metric Prefixes
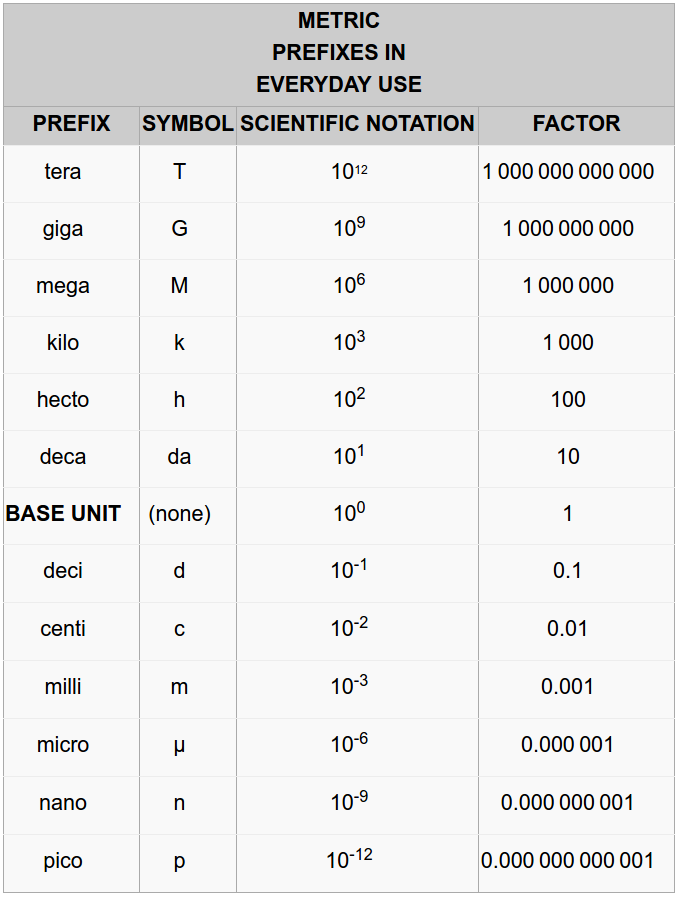
The value of the metric system is in the ease of converting from one multiple to another since everything is in base 10 compared to the Imperial system. º
Ex. 1000 mm = 1 m 1000m = 1 km compared to
12 in = 1 foot 3 feet = 1 yard 1760 yards = 1 mile
Metric conversions
Strategy for metric conversions
-
- What unit do you have to convert to?
- 500ml = ____L → liters
- What unit do you have to convert to?
-
- What unit are you starting from?
- 500ml → milliliters = ____L
- What unit are you starting from?
-
- Which unit is larger?
- Liters are the larger unit.
- Which unit is larger?
-
- By how much is that unit larger?
-
- Liters are 1,000X (103) greater than milliliters
- Milliliters are 1/1000 smaller than a liter
-
- By how much is that unit larger?
- Which direction are we moving? We are moving from a smaller to a larger unit (look at the table), so the value will be smaller. In this case, the value is smaller by 1,000X
In other words, the value is 1/1000 or 0.001 the value.
So what is the answer? ______________
You can try to visualize the conversions using a metric staircase. In the metric staircase each step represents a ten-fold change. If you move down the staircase you multiply your value by ten for each step or a move the decimal one place to the right for each step. If you move up the staircase you divide your value by ten for each or move the decimal point one place to the left for each step.
Try it for the example above going from 500ml to L.
Metric staircase
Factoring Out
Using the idea of factors of ten, you can assess the difference of the two units and cancel out the original unit algebraically to reach the desired final unit.
- 500ml=_____L
-
- 1ml =1000L or, 1L/1000ml both fraction state that there are 1000 milliliter in every 1 liter
- So 500ml X1L/1000ml = 500ml X 1L/1000ml = 500 X 1L/1000 = 500L/1000 = .5 L
-
pay attention to the units and how we’ve canceled out the ml in the numerator of 500ml and in the denominator in the conversion of 1L in 1000ml.
Scientists often work with numbers that are extremely large or extremely small. For example, there are 10,300,000,000,000,000,000,000 carbon atoms in a 1-carat diamond each of which has a mass of 0.000,000,000,000,000,000,000,020 grams. It is impossible to multiply these numbers with most calculators because they can’t accept either number as it is written here. To do a calculation like this, it is necessary to express these numbers in scientific notation, as a number between 1 and 10 multiplied by 10 raised to some exponent.
Exponent Review
Some of the basics of exponential mathematics are given below.
| Any number raised to the zero power is equal to 1. | 10= 1 | 100= 1 | ||||
| Any number raised to the first power is equal to itself. | 11 = 1 | 101 = 10 | |||
| Any number raised to the nth power is equal to the product of that number times itself n-1 times. | ||||||
| 22 = 2 x 2 = 4 | 105 = 10 x 10 x 10 x 10 x 10 = 100,000 | |||||
| Dividing by a number raised to an exponent is the same as multiplying by that number raised to an exponent of the opposite sign. |
The following rule can be used to convert numbers into scientific notation: The exponent in scientific notation is equal to the number of times the decimal point must be moved to produce a number between 1 and 10.
To translate 10,300,000,000,000,000,000,000 carbon atoms into scientific notation, we move the decimal point to the left 22 times.
10,300,000,000,000,000,000,000 = 1.03 x 1022
To convert numbers smaller than 1 into scientific notation, we have to move the decimal point to the right. The decimal point in 0.000985, for example, must be moved to the right four times.
0.000985 = 9.85 x 10-4
Converting 0.000000000000000000000020 grams per carbon atom into scientific notation involves moving the decimal point to the right 23 times.
0.000000000000000000000020 = 2.0 x 10-23
The primary reason for converting numbers into scientific notation is to make calculations with unusually large or small numbers less cumbersome. Because zeros are no longer used to set the decimal point, all of the digits in a number in scientific notation are significant, as shown by the examples.
Practice conversions (THIS CAN BE A H5p EXERCISE)
ACCURACY and PRECISION
In taking measurements using a particular method, it is important to know the limit of detectability, which is the smallest difference one can detect. The significant figures are the number of digits one can read directly using the measuring device. One can sometimes estimate an additional significant figure. Within the limit of detectability, accuracy is how close your measurement is to the true value. Your accuracy may be limited by the available technology. You may have to be satisfied with an approximation, which is a value that is not exact. Precision is the degree of agreement between several measurements. Your data may be precise but not necessarily accurate because of flaws in the procedure. In science, results obtained by one person need to be reproduced by others before they can be accepted. Artifacts may be introduced by external factors, leading to incorrect conclusions.
Accuracy refers to how closely a measured value agrees with the correct or target value.
Precision refers to how closely individual measurements agree with each other and reflects a repeatability in those measurements.
Instruments have a finite amount of accuracy and it is important to report measurements within that level of accuracy. Significant figures, report the number of digits that are known to some degree of confidence with the measuring device. With increased sensitivity of the equipment , the number of significant figures increases.
Here is an example which uses the above ideas:
Sue and Jane want to know the length of the hallway in front of their classroom. Sue used a piece of yarn that was 1 meter long. She took the measurement very carefully 3 times and came up with the numbers: 11.2 meters, 11.4 meters, and 11.3 meters. Sue took the average and concluded that the hallway is 11.3 meters long. Jane used a stick 1 meter long and took the measurement very carefully 3 times. She came up with the numbers: 12.4 meters, 12.6 meters, and 12.0 meters. Jane concluded that the hallway is 12.3 meters long. They learned from the architect later that the length of the hallway is 12.4 meters.
-
- 11.2 meters, 11.4 meters, 11.3 meters is Sue’s raw data.
-
- 12.4 meters, 12.6 meters, 12.0 meters is Jane’s raw data.
-
- Both Sue and Jane are aware of the limit of detectability using their instruments. They did not try to measure down to millimeters.
-
- The significant figures of their instruments are both 1 meter. They added an extra digit by estimation.
-
- Sue’s measurement is more precise than Jane’s.
-
- Sue’s measurement can not be reproduced by Jane.
-
- According to the data from the architect, Jane’s measurements are more accurate than Sue’s, although they are less precise.
- In trying to figure out why her measurements are not as accurate as Jane’s, Sue realized that she stretched the piece of yarn while measuring the hallway, thus introducing an artifact into her measurement, leading to an incorrect conclusion.
Lab Activity:
Length
Metric units of length measurement most commonly used in biology include the meter (m), centimeter (cm), millimeter (mm), micrometer (μm), and nanometer (nm)
How many cm are in a meter? _________
How many μm are in a millimeter? __________
How many mm are in a centimeter? _________ How many nm are in a micrometer? _________
Measuring with Metric
- Obtain a ruler. Find the metric ( centimeters and millimeters) and English units (inches).
How many millimeters are in 2 centimeters? 2 cm = ______ mm
How many centimeters in one inch? 1 in = _______cm
Use a meter stick or a metric ruler to measure the following:
Width of classroom door opening (in meters) _______ m
Length of blackboard (in meters) _______ m
Length of a dollar bill (in centimeters) _______ cm
Width of your pen (in millimeters) _______ mm
Width of a penny (in millimeters) _______ mm
Why is it preferable to measure a penny in millimeters rather than centimeters or meters?
The units micrometer (μm) and nanometer (nm) are useful in microscopy for measuring very tiny objects like cells or even viruses
THE SCIENTIFIC METHOD
The hypothetico-deductive approach underlies most sciences. The procedure has four stages:
(1) Observations. Events can be observed either as they occur naturally or as the result of experiments. In many cases, instruments such as microscopes or spectrophotometers are used.
(2) Forming hypotheses. A hypothesis is a theory designed to explain the observations. Assumptions are made in developing the hypothesis.
(3) Predictions can be made based on the hypothesis.
(4) Testing the predictions. Experiments are designed and performed to test the predictions. The experiments lead to new observations, beginning the cycle again, often leading to a modified hyptothesis.
Graphing exercises
Fetal Alcohol Syndrome is a serious birth defect that results from heavy drinking during pregnancy.
You are doing a study of I.Q. levels of 4th graders. You are testing two groups: Group A – children of mothers who drank less than 4 oz. of wine a day during pregnancy; Group B – children of mothers who drank up to a quart of wine a day (or its equivalent: a six pack of beer or 6 oz. of scotch.)
| Group A Children (I.Q.) | Group B Children (I.Q.) | |||||||
| 98 | 97 | 105 | 123 | 98 | 101 | 95 | 97 | |
| 102 | 100 | 118 | 107 | 86 | 99 | 96 | 105 | |
| 112 | 91 | 100 | 97 | 103 | 108 | 113 | 86 | |
| 86 | 96 | 115 | 105 | 106 | 92 | 95 | 107 | |
| 116 | 104 | 104 | 111 | 94 | 108 | 105 | 96 | |
Analyze the data by plotting histograms of both groups. Calculate the mean, median and mode I.Q. for both groups. What is your conclusion?
Lab Exercises





